rudless.

Que donne réellement \(\frac{x}{0}\)

J'imagine qu'on a déjà dû vous apprendre à effectuer la division d'un nombre par un autre, sinon vous ne chercherez pas un article sur la division par \(0\) en mathématique.

On a dû vous expliquer que lorsqu'on avait deux nombres \(x \ et \ y\) et que vous recherchez la valeur de \(\frac{x}{y}\), on cherche tout simplement le nombre de fois que \(y\) entre dans \(x\) qui vaut \(q\), appelé quotient de la division de \(x\ par \ y\), en termes simples. Sûrement oui!!!

La division par zéro est mathématiquement indéfinie et n'est pas définie dans le système des nombres réels standard. Lorsque vous divisez un nombre par zéro, cela conduit à une contradiction et ne peut pas être correctement évalué.

Pour illustrer cela, prenons un exemple simple : \(2\) divisé par \(0\). Si nous supposons que cela est égal à un certain nombre (par exemple \(x\)), alors \(2 = x \times 0\). Cependant, tout nombre multiplié par zéro est toujours égal à zéro, donc \(x\times 0 = 0\). Cela mène à une contradiction, car nous avons alors à la fois \(2 = 0\) et \(2 = x\times 0 = 0\). Cela montre qu'il n'y a pas de réponse unique ou définie à la division par \(0\).

En mathématiques, lorsqu'un calcul implique une division par \(0\), cela est considéré comme une erreur et le résultat n'est pas défini.
Illustrons tout cela....

Exemples

• \(\frac{10}{5}=2\)
  

  On dira alors que dans \(10\), il y a \(2\) paquets de \(5\).

• \(\frac{10}{2}=5\)
  

  On dira alors que dans \(10\), il y a \(5\) paquets de \(2\).

Bon, c'est pas mal.

Alors, on gobe ça, ça marche très bien mais on ne nous explique pas toujours ce que cela signifie réellement.

Je ne sais pas vous mais personnellement, je n'aime pas apprendre bêtement des choses. J'ai besoin de comprendre. Une fois que j'ai assimilé la logique, je retiens beaucoup plus facilement que du par-cœur car du coup, ça fait sens.

Bien sûr, ce n'est pas un savoir caché et certains professeurs l'expliquent et c'est génial. Mais avec la pression du programme et le peu de temps qu'on a pour le faire, certains ont tendance à aller à l'essentiel en donnant les outils sans mentionner pourquoi ils marchent.

Sans plus tarder, passons à l'essentiel.

Premier raisonnement

En réalité,d'après ce raisonnement, la division est une succession de soustractions; cest-à-dire,diviser nombre \(x\) par \(y\) revient à trouver le nombre de fois qu'on
doit soustraire \(y\) à \(x\) pour avoir plus rien, donc \(0\).

En conséquence, si \(\frac{x}{y}=q\),alors \(q\) est le nombre de fois qu'on doit soustraire \(y\) à \(x\) pour avoir \(0\).

Exemples

• \(\frac{10}{5}=2\)

On dirait alors que si \(\frac{10}{2}=2\), alors \(2\) est le nombre de fois qu'on doit soustraire \(5\) à \(10\) pour avoir \(0\);
cest-à-dire \(\frac{10}{2}=2\implies 10-\underbrace{5-5}_{\mathrm{2\ fois}}\)

• \(\frac{10}{2}=5 \implies 10-\underbrace{2-2-2-2-2}_{\mathrm{5\ fois}}\)
• \(\frac{10}{1}=10 \implies 10-\underbrace{1-1-1-1-1-1-1-1-1-1}_{\mathrm{10\ fois}}\)
• \(\frac{10}{0}=\infty \implies 10-\underbrace{0-0-0\ldots -0-0-0\ldots}_{\mathrm{\infty}}\)

Second raisonnement

Prenons \(\frac{10}{1}=10 \)
Approchons-nous des valeurs les plus proches de \(0\)
Nous aurons :

• \(\frac{10}{0,1}=100\)
• \(\frac{10}{0,01}=1000\)
• \(\frac{10}{0,001}=1000\)

Nous remarquons alors que plus nous divisons \(10\) par des valeurs les plus proches de \(0\), notre quotient tend à exploser et à devenir plus grand.

Supposons maintenant que nous avons atteint \(0\). Qu'aurons-nous en divisant \(10\ par \ 0\)?
Sans doute \(\frac{10}{0}=\infty\), partant de ce principe.

Voici la représentation graphique :

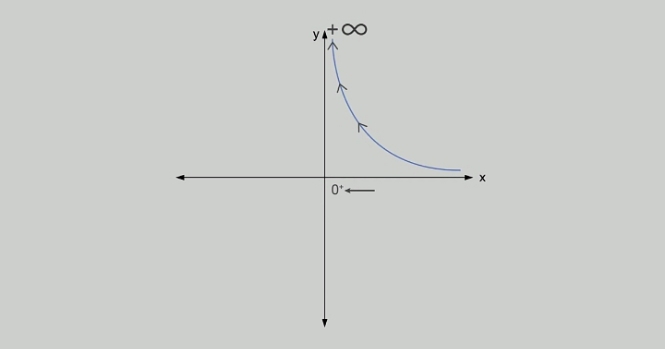
Cette représentation nous dit que lorsque \(x\) s'approchent de \(0\) par des valeurs positives, les \(y\) tendent vers \(+\infty\)

Mais si nous nous limitons là,nous faisons face à un sérieux problème. Lequel?

Si \(\frac{10}{0}=\infty\), alors pour tout nombre \(x\), \(\frac{x}{0}=\infty\)? Si oui,
Supposons que \(x=1 \ et\ x=10\), alors

Nous voici devant un autre problème.
On a trouvé que \(\frac{1}{0}=\infty\) et \(\frac{10}{0}=\infty\). Donc on peut dire que \(\frac{1}{0}=\infty=\frac{10}{0}=\infty\)

Si ces deux fractions sont identiques et qu'elles ont le même dénominateur, cela revient à dire que leurs numérateurs aussi sont égaux.
Donc \(\frac{1}{0}=\frac{10}{0} \iff 10=1\)

Ce qui est complètement bête et absurde

Ainsi, si \(1O\ne1\), donc \(\frac{1}{0}\ne\frac{10}{0}\); \(\frac{1}{0}=\infty\ne\frac{10}{0}=\infty\); \(\frac{1}{0}\ne\infty\) et \(\frac{10}{0}\ne\infty\)

Donc \(\frac{10}{0}\) ne peut pas donner seulement \(\infty\); il en est de même pour \(\frac{1}{0}\)

Euh!!!!!! Alors cela donne quoi exactement?

Nous allons essayer de trouver cette vraie valeur grâce à une méthode simple et claire.

Soit \(y=f(x) \ : \ f(x)=\frac{10}{x} \) qui est une fonction rationnelle.

En réalité, cette fonction cache deux faces. La première fait penser à des \(x\) positifs et la deuxième aux \(x\) négatifs

La première :

Voici la représentation graphique de la première :

La deuxième :

Contradiction totale :

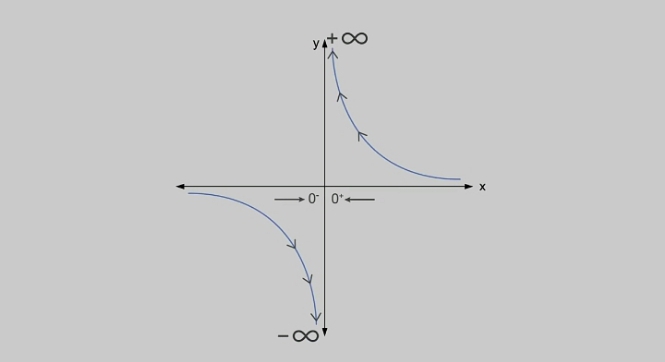
Ceci nous dit que lorsque les \(x\) s'approchent de \(0\) par des valeurs positives, les \(y\)tendent vers \(+\infty\) et lorsque
les \(x\) s'approchent de \(0\) par des valeurs négatives, les \(y\)tendent vers \(-\infty\)

Ceci nous amène à dire que la division d'un nombre par \(0\) n'est pas définie car on ne sait pas si on va vers \(+\infty\) ou vers \(-\infty\)

En terme des limites

Nous savons que la limite d'une fonction rationnelle lorsque \(x\) tend vers \(0\) existe lorsque la limite à gauche de cette fonction est égale à sa limite à droite.

Testons cette condition avec notre fonction \(f(x)=\frac{10}{x}\). Il est clair que cette limite n'existe pas. car :
\(\underset{x\to 0^+}{lim \frac{10}{x}}=+\infty\) et \(\underset{x\to 0^-}{lim \frac{10}{x}}=-\infty\)
Puisque \(\underset{x\to 0^+}{lim \frac{10}{x}}=+\infty\ne \underset{x\to 0^-}{lim \frac{10}{x}}=-\infty\); cest-à-dire \(\underset{x\to 0^+}{lim \frac{10}{x}}\ne \underset{x\to 0^-}{lim \frac{10}{x}}\), alors on conclut que \(\underset{x\to 0}{lim \frac{10}{x}}\nexists\)