

UNITES D'ANGLES
ANGLES
1. Définition
Un angle est la surface illimité comprise entre deux demi-droites de même origine. Cette origine est appelée sommet de l'angle.
Exemple
2. Mesure d'angle
\(\blacklozenge\) L'ouverture entre deux côtés d'un angle s'appelle l'amplitude .
L'amplitude se mesure en degré à l'aide d'un rapporteur.
\(\blacklozenge\) Un angle droit est un angle dont les côtes sont perpendiculaires.
\(\blacklozenge\) Deux sous-multiples de l'angle droit sont souvent d'usage pour mesurer les angles.
Le degré
Il est la \(90^e\) partie d'angle droit, c'est-à-dire la \(360^e\) partie d'un angle plein.
Ce sont des astronautes Babyloniens qui avaient décidé de diviser l'angle plein en 360 parties. Le degré est noté "°".
Le rapporteur est un instrument de mesure d'angle gradué en degré.
Sous-multiples de degré
-
La minute : Elle est la \(60^e\) partie du degré.
\(\begin{array}{|c|lcccr|} \hline 1°=60'\\ \hline \end{array}\) -
La seconde : Elle est la \(60^e\) partie de la minute.
\(\begin{array}{|c|lcccr|} \hline 1'=60''\\ \hline \end{array}\)
\(\begin{array}{|c|lcccr|} \hline 1°=3600''\\ \hline \end{array}\)
Le grade
Le grade est la \(100^e\) partie d'un angle droit. C'est en 1803 qu'on décida qu'un angle droit mesurerait \(100\) grades. Le grade est noté "gr"
Les sous-multiples de grade
- Le decigrade (degr)
- Le centigrade (cgr)
- Le milligrade (mgr) \(1gr=10dgr=100cgr=1000mgr\)
RELATIONS ENTRE LES DIFFERENTES UNITES D'ANGLE
Un angle droit \(=90^°=100gr\)
Le radian
Dans un cercle, à tout angle au centre correspond un arc sur la circonférence. A un angle au centre droit, correspond un quadrant et à l'angle au centre plein correspond une circonférence entière.
Mesurer l'amplitude d'un angle par la longueur de l'arc qui lui correspond sur un cercle centré en son sommet revient à choisir une nouvelle unité pour mesurer l'amplitude d'un angle.
L'angle qui intercepte l'arc de longueur égal aux rayons. Cette unité s'appelle Radian (Rad).
La circonférence \(=2\pi Rad\)
\(360°=2\pi Rad\)
\(1 rad=\frac{360°}{2\pi}=\frac{180°}{\pi}\)
\(1 rad=57,3°\)
\(1°=\frac{2\pi Rad}{360°}\simeq 0,01744 Rad \\ =\frac{2.3,14}{360°}\simeq 0,017 Rad\)
Remarques
La mesure d'un angle donné sans unités, sous-entend radian
Exemple
\(90°=\frac{\pi R}{2}\) ou tout simplement \(\frac{\pi}{2}\)
Conversation des unités d'angles
\( \left\{ \begin{aligned} 90°=100 gr\\ 360°=2\pi R\\ 1°=60'\\ 1'=60''\\ \end{aligned} \right. \)En fait, ces relations permettent une conversation d'une unité en une autre, en utilisant la règle de 3 simples ou la loi de proportion.
Si vous avez des difficultés sur cette notion, je vous invite à suivre mon cours sur l'ensemble \(\mathbb{R}\) juste par ici pour la notion des proportions et ici pour la règle de trois simple afin d'en savoir plus. Merci !
1. Convertir \(n°\) en radian(s)
\(360°\to 2\pi R\)\(1°\to \frac{2\pi R}{360°}\)
\(\begin{array}{|c|lcccr|} \hline n°\to \frac{2\pi R\times n}{360°}\\ \hline \end{array}\)
Ainsi,
\(180°\to \frac{2\pi R\times 180}{360}=\frac{2.180\pi}{360}=\frac{360\pi}{360}=\pi\)
\(60°\)
\(45°\to \frac{2\pi\times 45}{360}=\frac{90\pi}{360}=\frac{\pi}{4} \)
\(30°\to \frac{2\pi\times 30}{360}=\frac{60\pi}{360}=\frac{\pi}{6} \)
1. Convertir \(n°\) en grade
\(90°=100 gr\)
\(10°=\frac{100gr}{90}=\frac{10}{9}gr\)
\(\begin{array}{|c|lcccr|}
\hline
n° = \frac{10\times n}{9} gr\\
\hline
\end{array}\)
Ainsi
\(5°\to \frac{10\times 5}{9}=\frac{50}{9} gr\)
\(1,5°\to \frac{10\times 1?5}{9}=\frac{15}{9}=\frac{5}{3} gr \)
\(1000°\to \frac{10\times 1000}{9}=\frac{10000}{9} gr \)
Convertir \(n\) degré(s) en grade(s)
\(100 gr=90°\)
\(1 gr=\frac{90}{100}=\frac{9}{10}° \)
\(\begin{array}{|c|lcccr|}
\hline
n gr=\frac{9\times n}{10}\\
\hline
\end{array}\)
Ainsi
\(5 gr\to \frac{9\times 5}{10}=\frac{45}{10}=4,5° \)
\(11 gr\to \frac{9\times 11}{10}=\frac{99}{10}=9,9° \)
Convertir \(n\) radian(s) en grade(s)
\(\begin{array}{|c|lcccr|}
\hline
\frac{\pi}{2}=100 gr\\
\hline
\end{array}\)
\(\frac{4\pi}{2}=4\times 100 gr \)
Conversation \(n°\) en minute(s), seconde(s)
\( 1°=60'=3600' \)
\(30°=30.60'=30.3600''\\ 1800'=108000'' \)
\(30,5°=30°+0,5° \\ = 30°+30' \\ 1800+30' \\ 1830' \)
\(22,869°= 22°\ 52,14\\ = 22°52',8'' \\ = 22\times 60+52'+8''\\ = 1372'8'' \)
Angle inscrit et angle au centre
1. Angle inscrit
Un angle est inscrit à un cercle si son sommet appartient à ce cercle et si les deux demi-droites (côtés issus de ce sommet) coupent le cercle une deuxième fois.
Exemple
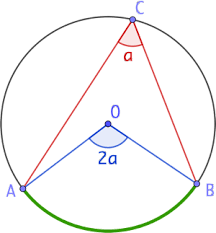
L'angle \(\widehat{ACB}\) de la figure ci-dessus est un angle inscrit au cercle.
On dit que l'angle \(\widehat{ACB}\) intercepte l'arc \(\widehat{AB}\) qui ne contient pas le point \(C\).
2. Angle au centre
Un angle au centre d'un cercle a le centre de ce cercle comme sommet.
Exemple

L'angle \(\widehat{A0B}\) de la figure ci-dessus est un angle au centre.
THEOREME DE PYTHAGORE
Théorème de Pythagore en terme d'aires
Le premier théorème dit : l'aire d'un carré construit sur l'hypoténuse
d'un triangle rectangle égale la
somme des aires des carrés construits sur les autres côtés.
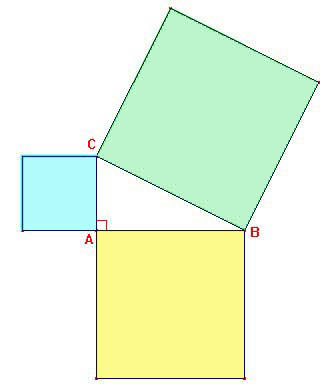
ce théorème permet de calculer la longueur d'u côté d'un triangle rectangle, connaissant la longueur de deux autres côtés.
L'égalité \(c^2=a^2+b^2 \) entraîne les égalités :
\( c=\sqrt{a^2+b^2} \)
\( a=\sqrt{c^2-b^2} \)
\( b=\sqrt{c^2-a^2} \)
Exemple
Un des côtés de l'angle droit d'un triangle rectangle mesure \(4cm\) et l'hypoténuse mesure \(5cm\). Quelle est la mesure de l'autre côté de l'angle droit?
Résolution
Le triangle étant rectangle, le théorème de Pythagore donne : \( c=\sqrt{a^2+b^2} \), \( b=\sqrt{c^2-a^2} \)
\(c^2=a^2+b^2 \iff c=\sqrt{a^2+b^2} \iff b=\sqrt{c^2-a^2}\)
\(b=\sqrt{25-16} \\ = \sqrt{9} \\ =3\)
Donc la mesure de l'autre côté decet angle droit est de \(3cm\).
Théorème de Pythagore en terme de longueur
Pour exprimer une relation entre les longueurs des côtés d'un triangle rectangle, on reformule les
énoncés précédents (Théorème \(1\)) de la manière suivante :
Le carré de la longueur de l'hypothénuse d'un triangle rectangle
est égal à la somme des carrés des longueurs de deux autres côtés.
\(c^2=a^2+b^2 \)
Réciproque du Théorème de Pythagore
Si dans un triangle, le carré de la longueur d'un côté est égal à la somme des carrés des longueurs de deux autres côtés, alors le triangle est rectangle.
Exemple
Soit le triangle \(ABC\) dont les côtés ont pour longueurs \(a=3cm, b=4cm\ et \ c=5cm\).
Montrer que ce triangle est rectangle est que \(c\) est la mesure de son hypothénuse.
Résolution
Pour qu'un triangle soit rectangle, il suffit que le carré de la longueur la plus grande soit égale à la somme des carrés des longueurs de deux autres côtés.
La relation entre les carrés des mesures des \(3\) côtés \(c,a\ et \ b\) est :
\(25=16+9\)
Ce qui établit la relation de Pythagore. Par conséquent, le triangle \(ABC\) est donc rectangle et le côté de la longueur \(5cm\) est
l'hypoténuse.
APPLICATION DU THEORME DE PYTHAGORE
Longueur de la diagonale d'un triangle rectangle
Dans un rectangle, une diagonale est un segment de droite qui joint deux sommets non consécutifs et qui divise le rectangle en deux triangles rectangles isométriques.
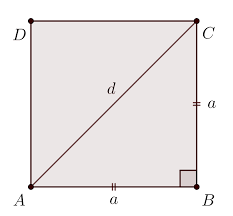
La diagonale \(d\) du rectangle \(ABCD\) est l'hypoténuse commune aux deux rectangles \(ABCD\).
En vertu du théorème de Pythagore, on a :
\(d^2=a^2+b^2\)
\(d=\sqrt{a^2+b^2}\)
Exemples
\(1.\) Des mesures de dimension d'un rectangle sont \(12cm\ et \ 15cm\). Calculer la mesure de la diagonale de ce rectangle.
Résolution
Conformément au théorème de Pythagore, on a :
\(d=\sqrt{a^2+b^2} \\ =\sqrt{5ç2+12^2} \\ =\sqrt{25+144} \\ = \sqrt{169}\\ =13cm \)
\(2.\) La longueur de la diagonale d'un carré de \(10cm\) de côtés est :
Résolution
\(d=\sqrt{a^2+b^2}\)
\(\sqrt{10^2+10^2} \\ =\sqrt{100} \\=\sqrt{2.100}\\=10\sqrt{2} \)
hauteur d'un triangle équilatéral
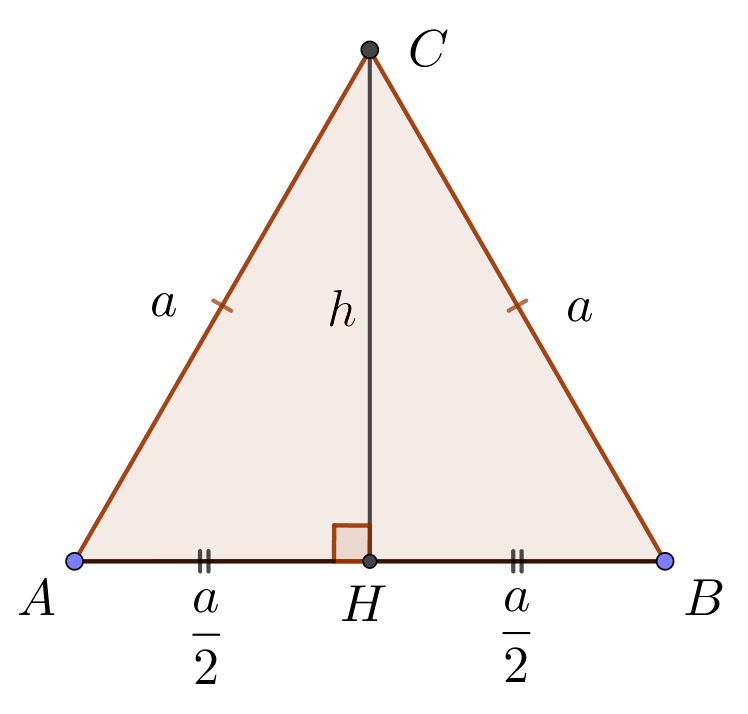
Soit le triangle équilatéral \(ABC\) et \(a\) la longueur du côté. La hauteur \(h\)divise le triangle \(ABC\) en deux rectangles \(T_1\ et \ T_2\).
Le théorème de Pythagore permet d'écrire :
\(a^2=h^2+(\frac{a}{2})^2 \)
De cette relation, on tire la hauteur :
\(a^2=h^2+(\frac{a}{2})^2 \)
\(-h^2=-a^2+\frac{a^2}{4} \)
\(h^2=a^2-\frac{a^2}{4} \\ = \frac{4a^2-a^2}{4}\\= \frac{3a^2}{4} \)
\(h^2=\frac{3a^2}{4} \)
\(h=\sqrt{\frac{3a^2}{4}} \)
\(h=\sqrt{\frac{\sqrt{3a^2}}{4}} \)
\(h=\sqrt{\frac{3a^2}{2}} \)
\(\begin{array}{|c|lcccr|}
\hline
h=a\sqrt{\frac{3}{2}}\\
\hline
\end{array}\)
Exemple
La longueur d'un triangle équilatéral de \(4cm\) de côtés est ?
Résolution
\(h=a\sqrt{\frac{3}{2}} \\ =4\sqrt{\frac{3}{2}}\\ = 2\sqrt{3}cm \)Longueur de la diagonale d'un parallélipipède rectangle
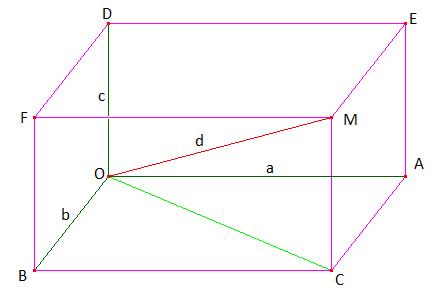
\(d^2=a^2+b^2+c^2\)
\(d=\sqrt{a^2+b^2+c^2}\)
Exemple
Calculer la longueur de la diagonale d'un parallélipipède rectangle dont les longueurs de dimension de la base sont \(6cm\ et \ 4cm\) et la hauteur (deux) \(2cm\).
Résolution
\(d=\sqrt{a^2+b^2+c^2}\)
\(d=\sqrt{6^2+4^2+2^2} \\ = \sqrt{36+16+4} \\ = \sqrt{56} \\ = 7,4cm\)